Canadian examples Cognitive Examples

First order differential equations problems and solutions pdf
A solution of a first order differential equation is a function f(t) that makes F(t,f(t),f ′ (t)) = 0 for every value of t. Here, F is a function of three variables which we label t, y, and ˙y.
6 I. Setting Up First-Order Differential Equations from Word Problems derivative at each point on a curve and where the curve begins, then you can reconstruct this solution curve.
(1) First order equations: Variable-Separable Method. (2) Existence and uniqueness of solutions to initial value problems. (3) Continuation of solutions, Saturated solutions, and …
Differential equations arise in many problems in physics, engineering, and other sciences. The following examples show how to solve differential equations in a few simple cases when an exact solution exists. Separable first-order ordinary differential equations. Equations in the form = () are called separable and solved by () = and thus ∫ = ∫ (). Prior to dividing by (), one needs to check
studied a variety of second order linear equations and they have saved us the trouble of finding solutions to the differential equations that often ap- pear in applications.
Ch 3.1: Second Order Linear Homogeneous Equations with Constant Coefficients A Consider the second order linear initial value problem where p, q are continuous on an open interval I containing t 0. In light of the initial conditions, note that y = 0 is a solution to this homogeneous initial value problem. Since the hypotheses of Theorem 3.2.1 are satisfied, it follows that y = 0 is the
FIRST-ORDER ORDINARY DIFFERENTIAL EQUATIONS G ⇒ geometric interpretation of solutions ♦ Equations of higher order may be reduceable to first-order problems in special cases — e.g. when y or x variables are missing from 2nd order equations. …
Solving First Order Linear Equations Today we will discuss how to solve a first order linear equation. Our technique will require close familiarity with the product and chain rules for derivatives, so we will
First Order Differential Equations Practice Problem with Solutions FAQ PDF Download. Learn first order differential equations practice problem with solutions FAQ, engg math FAQ, competency based interview questions with MCQs based online test prep.
The final chapter deals with first-order differential equations. This book is a valuable resource for mathematicians, graduate students, and research workers. Table of Contents. Participants Preface I. Invited Papers A General Approach to Linear Problems for Nonlinear Ordinary Differential Equations Differential Relations Conditions for Boundedness of Systems of Ordinary Differential Equations
Understand what the finite difference method is and how to use it to solve problems. What is the finite difference method? called boundary-value problems. In this chapter, we solve second-order ordinary differential equations of the form . f x y y a x b dx d y = ( , , ‘), ≤
the equation into something soluble or on nding an integral form of the solution. First order PDEs a @u @x +b @u @y = c: Linear equations: change coordinate using (x;y), de ned by the characteristic equation dy dx = b a; and ˘(x;y) independent (usually ˘= x) to transform the PDE into an ODE. Quasilinear equations: change coordinate using the solutions of dx ds = a; dy ds = b and du ds = c …
Every rst order di erential equation to be considered here can be written can be written in the form P(x;y) usually guarantee that a di erential equation has a solution, in practice the solutions can seldom be written in closed form.” (I.e. there is no actual formula for the solution.) Thus the equations that are dealt with here are actually the exceptional ones. There are ve kinds of rst
Linear Differential Equations of First Order. Page 1 Problems 1-2. Page 2 Problems 3-7. Definition of Linear Equation of First Order. A differental equation of type [y’ + aleft( x right)y = fleft( x right),] where (aleft( x right)) and (fleft( x right)) are continuous functions of (x,) is called a linear nonhomogeneous differential equation of first order. We consider two
Study differential equations questions with solutions online courses with multiple choice question (MCQs): wronskian is a, for bachelor degree and masters degree questions with choices difference, integration, determinant, differentiation with problem solving answer key to test study skills for online e-learning, formative assessment and jobs’ interview preparation tips. Learn second order
SECTION 15.1 Exact First-Order Equations 1093 Exact Differential Equations • Integrating Factors Exact Differential Equations In Section 5.6, you studied applications of differential equations to growth and decay problems. In Section 5.7, you learned more about the basic ideas of differential equa-tions and studied the solution technique known as separation of variables. In this chapter, you
24 CHAPTER 2. METHODS FOR SOLVING FIRST ORDER ODES Solution: In this problem, M = ye xy and N = xe xy +sin y. Thus, My = exy +xye xy and Nx = exy +xye xy, which implies that the differential equation is exact.
In this section we solve linear first order differential equations, i.e. differential equations in the form y’ + p(t) y = g(t). We give an in depth overview of the process used to solve this type of differential equation as well as a derivation of the formula needed for the integrating factor used in the solution …
On the Cauchy Problem for First Order Discontinuous
https://www.youtube.com/embed/eP9UZGwbVZM

Solutions of First-Order Volterra Type Linear
The numerical solutions of linear integrodifferential equations of Volterra type have been considered. Power series is used as the basis polynomial to approximate the solution of the problem. Furthermore, standard and Chebyshev-Gauss-Lobatto collocation points were, respectively, chosen to collocate
Download the differential equations PDF here and learn about Differential equation solutions,Differential equations formulas and first order differential equations.Differential equations are mathematical equations that contain second derivatives.
FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I: Introduction and Linear Systems David Levermore Department of Mathematics University of Maryland
Differential Equations Problems With Solutions Pdf main ideas to solve certain differential equations, like first order scalar hence solutions to the

https://www.youtube.com/embed/zDcXt9Vx34o

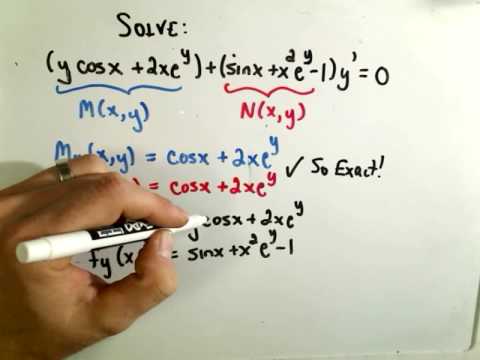
https://www.youtube.com/embed/tF9eEGs8aao

Differential Equations Questions with Solutions Engg
First Order Differential Equations Practice Problem with

(1) First order equations: Variable-Separable Method. (2) Existence and uniqueness of solutions to initial value problems. (3) Continuation of solutions, Saturated solutions, and …
FIRST-ORDER ORDINARY DIFFERENTIAL EQUATIONS G ⇒ geometric interpretation of solutions ♦ Equations of higher order may be reduceable to first-order problems in special cases — e.g. when y or x variables are missing from 2nd order equations. …
FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I: Introduction and Linear Systems David Levermore Department of Mathematics University of Maryland
Download the differential equations PDF here and learn about Differential equation solutions,Differential equations formulas and first order differential equations.Differential equations are mathematical equations that contain second derivatives.
Ch 3.1: Second Order Linear Homogeneous Equations with Constant Coefficients A Consider the second order linear initial value problem where p, q are continuous on an open interval I containing t 0. In light of the initial conditions, note that y = 0 is a solution to this homogeneous initial value problem. Since the hypotheses of Theorem 3.2.1 are satisfied, it follows that y = 0 is the
SECTION 15.1 Exact First-Order Equations 1093 Exact Differential Equations • Integrating Factors Exact Differential Equations In Section 5.6, you studied applications of differential equations to growth and decay problems. In Section 5.7, you learned more about the basic ideas of differential equa-tions and studied the solution technique known as separation of variables. In this chapter, you
6 I. Setting Up First-Order Differential Equations from Word Problems derivative at each point on a curve and where the curve begins, then you can reconstruct this solution curve.
Differential equations arise in many problems in physics, engineering, and other sciences. The following examples show how to solve differential equations in a few simple cases when an exact solution exists. Separable first-order ordinary differential equations. Equations in the form = () are called separable and solved by () = and thus ∫ = ∫ (). Prior to dividing by (), one needs to check
A solution of a first order differential equation is a function f(t) that makes F(t,f(t),f ′ (t)) = 0 for every value of t. Here, F is a function of three variables which we label t, y, and ˙y.

Solutions of First-Order Volterra Type Linear
On the Cauchy Problem for First Order Discontinuous

SECTION 15.1 Exact First-Order Equations 1093 Exact Differential Equations • Integrating Factors Exact Differential Equations In Section 5.6, you studied applications of differential equations to growth and decay problems. In Section 5.7, you learned more about the basic ideas of differential equa-tions and studied the solution technique known as separation of variables. In this chapter, you
FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I: Introduction and Linear Systems David Levermore Department of Mathematics University of Maryland
6 I. Setting Up First-Order Differential Equations from Word Problems derivative at each point on a curve and where the curve begins, then you can reconstruct this solution curve.
(1) First order equations: Variable-Separable Method. (2) Existence and uniqueness of solutions to initial value problems. (3) Continuation of solutions, Saturated solutions, and …
First Order Differential Equations Practice Problem with Solutions FAQ PDF Download. Learn first order differential equations practice problem with solutions FAQ, engg math FAQ, competency based interview questions with MCQs based online test prep.
Understand what the finite difference method is and how to use it to solve problems. What is the finite difference method? called boundary-value problems. In this chapter, we solve second-order ordinary differential equations of the form . f x y y a x b dx d y = ( , , ‘), ≤
The numerical solutions of linear integrodifferential equations of Volterra type have been considered. Power series is used as the basis polynomial to approximate the solution of the problem. Furthermore, standard and Chebyshev-Gauss-Lobatto collocation points were, respectively, chosen to collocate
FIRST-ORDER ORDINARY DIFFERENTIAL EQUATIONS G ⇒ geometric interpretation of solutions ♦ Equations of higher order may be reduceable to first-order problems in special cases — e.g. when y or x variables are missing from 2nd order equations. …
Differential equations arise in many problems in physics, engineering, and other sciences. The following examples show how to solve differential equations in a few simple cases when an exact solution exists. Separable first-order ordinary differential equations. Equations in the form = () are called separable and solved by () = and thus ∫ = ∫ (). Prior to dividing by (), one needs to check
In this section we solve linear first order differential equations, i.e. differential equations in the form y’ p(t) y = g(t). We give an in depth overview of the process used to solve this type of differential equation as well as a derivation of the formula needed for the integrating factor used in the solution …
studied a variety of second order linear equations and they have saved us the trouble of finding solutions to the differential equations that often ap- pear in applications.

FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I
Differential Equations Questions with Solutions Engg

FIRST-ORDER ORDINARY DIFFERENTIAL EQUATIONS G ⇒ geometric interpretation of solutions ♦ Equations of higher order may be reduceable to first-order problems in special cases — e.g. when y or x variables are missing from 2nd order equations. …
Ch 3.1: Second Order Linear Homogeneous Equations with Constant Coefficients A Consider the second order linear initial value problem where p, q are continuous on an open interval I containing t 0. In light of the initial conditions, note that y = 0 is a solution to this homogeneous initial value problem. Since the hypotheses of Theorem 3.2.1 are satisfied, it follows that y = 0 is the
Linear Differential Equations of First Order. Page 1 Problems 1-2. Page 2 Problems 3-7. Definition of Linear Equation of First Order. A differental equation of type [y’ aleft( x right)y = fleft( x right),] where (aleft( x right)) and (fleft( x right)) are continuous functions of (x,) is called a linear nonhomogeneous differential equation of first order. We consider two
Differential equations arise in many problems in physics, engineering, and other sciences. The following examples show how to solve differential equations in a few simple cases when an exact solution exists. Separable first-order ordinary differential equations. Equations in the form = () are called separable and solved by () = and thus ∫ = ∫ (). Prior to dividing by (), one needs to check
6 I. Setting Up First-Order Differential Equations from Word Problems derivative at each point on a curve and where the curve begins, then you can reconstruct this solution curve.
24 CHAPTER 2. METHODS FOR SOLVING FIRST ORDER ODES Solution: In this problem, M = ye xy and N = xe xy sin y. Thus, My = exy xye xy and Nx = exy xye xy, which implies that the differential equation is exact.
Solving First Order Linear Equations Today we will discuss how to solve a first order linear equation. Our technique will require close familiarity with the product and chain rules for derivatives, so we will
(1) First order equations: Variable-Separable Method. (2) Existence and uniqueness of solutions to initial value problems. (3) Continuation of solutions, Saturated solutions, and …
Download the differential equations PDF here and learn about Differential equation solutions,Differential equations formulas and first order differential equations.Differential equations are mathematical equations that contain second derivatives.
The numerical solutions of linear integrodifferential equations of Volterra type have been considered. Power series is used as the basis polynomial to approximate the solution of the problem. Furthermore, standard and Chebyshev-Gauss-Lobatto collocation points were, respectively, chosen to collocate
Every rst order di erential equation to be considered here can be written can be written in the form P(x;y) usually guarantee that a di erential equation has a solution, in practice the solutions can seldom be written in closed form.” (I.e. there is no actual formula for the solution.) Thus the equations that are dealt with here are actually the exceptional ones. There are ve kinds of rst
A solution of a first order differential equation is a function f(t) that makes F(t,f(t),f ′ (t)) = 0 for every value of t. Here, F is a function of three variables which we label t, y, and ˙y.
Study differential equations questions with solutions online courses with multiple choice question (MCQs): wronskian is a, for bachelor degree and masters degree questions with choices difference, integration, determinant, differentiation with problem solving answer key to test study skills for online e-learning, formative assessment and jobs’ interview preparation tips. Learn second order
First Order Differential Equations Practice Problem with Solutions FAQ PDF Download. Learn first order differential equations practice problem with solutions FAQ, engg math FAQ, competency based interview questions with MCQs based online test prep.
The final chapter deals with first-order differential equations. This book is a valuable resource for mathematicians, graduate students, and research workers. Table of Contents. Participants Preface I. Invited Papers A General Approach to Linear Problems for Nonlinear Ordinary Differential Equations Differential Relations Conditions for Boundedness of Systems of Ordinary Differential Equations

On the Cauchy Problem for First Order Discontinuous
Differential Equations Questions with Solutions Engg

(1) First order equations: Variable-Separable Method. (2) Existence and uniqueness of solutions to initial value problems. (3) Continuation of solutions, Saturated solutions, and …
First Order Differential Equations Practice Problem with Solutions FAQ PDF Download. Learn first order differential equations practice problem with solutions FAQ, engg math FAQ, competency based interview questions with MCQs based online test prep.
FIRST-ORDER ORDINARY DIFFERENTIAL EQUATIONS G ⇒ geometric interpretation of solutions ♦ Equations of higher order may be reduceable to first-order problems in special cases — e.g. when y or x variables are missing from 2nd order equations. …
A solution of a first order differential equation is a function f(t) that makes F(t,f(t),f ′ (t)) = 0 for every value of t. Here, F is a function of three variables which we label t, y, and ˙y.
Solving First Order Linear Equations Today we will discuss how to solve a first order linear equation. Our technique will require close familiarity with the product and chain rules for derivatives, so we will
Differential Equations Problems With Solutions Pdf main ideas to solve certain differential equations, like first order scalar hence solutions to the
the equation into something soluble or on nding an integral form of the solution. First order PDEs a @u @x b @u @y = c: Linear equations: change coordinate using (x;y), de ned by the characteristic equation dy dx = b a; and ˘(x;y) independent (usually ˘= x) to transform the PDE into an ODE. Quasilinear equations: change coordinate using the solutions of dx ds = a; dy ds = b and du ds = c …
Linear Differential Equations of First Order. Page 1 Problems 1-2. Page 2 Problems 3-7. Definition of Linear Equation of First Order. A differental equation of type [y’ aleft( x right)y = fleft( x right),] where (aleft( x right)) and (fleft( x right)) are continuous functions of (x,) is called a linear nonhomogeneous differential equation of first order. We consider two
The numerical solutions of linear integrodifferential equations of Volterra type have been considered. Power series is used as the basis polynomial to approximate the solution of the problem. Furthermore, standard and Chebyshev-Gauss-Lobatto collocation points were, respectively, chosen to collocate
Differential equations arise in many problems in physics, engineering, and other sciences. The following examples show how to solve differential equations in a few simple cases when an exact solution exists. Separable first-order ordinary differential equations. Equations in the form = () are called separable and solved by () = and thus ∫ = ∫ (). Prior to dividing by (), one needs to check
The final chapter deals with first-order differential equations. This book is a valuable resource for mathematicians, graduate students, and research workers. Table of Contents. Participants Preface I. Invited Papers A General Approach to Linear Problems for Nonlinear Ordinary Differential Equations Differential Relations Conditions for Boundedness of Systems of Ordinary Differential Equations

First Order Differential Equations Practice Problem with
Solutions of First-Order Volterra Type Linear

FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I: Introduction and Linear Systems David Levermore Department of Mathematics University of Maryland
In this section we solve linear first order differential equations, i.e. differential equations in the form y’ p(t) y = g(t). We give an in depth overview of the process used to solve this type of differential equation as well as a derivation of the formula needed for the integrating factor used in the solution …
The numerical solutions of linear integrodifferential equations of Volterra type have been considered. Power series is used as the basis polynomial to approximate the solution of the problem. Furthermore, standard and Chebyshev-Gauss-Lobatto collocation points were, respectively, chosen to collocate
Solving First Order Linear Equations Today we will discuss how to solve a first order linear equation. Our technique will require close familiarity with the product and chain rules for derivatives, so we will
Download the differential equations PDF here and learn about Differential equation solutions,Differential equations formulas and first order differential equations.Differential equations are mathematical equations that contain second derivatives.
Understand what the finite difference method is and how to use it to solve problems. What is the finite difference method? called boundary-value problems. In this chapter, we solve second-order ordinary differential equations of the form . f x y y a x b dx d y = ( , , ‘), ≤
studied a variety of second order linear equations and they have saved us the trouble of finding solutions to the differential equations that often ap- pear in applications.
6 I. Setting Up First-Order Differential Equations from Word Problems derivative at each point on a curve and where the curve begins, then you can reconstruct this solution curve.
24 CHAPTER 2. METHODS FOR SOLVING FIRST ORDER ODES Solution: In this problem, M = ye xy and N = xe xy sin y. Thus, My = exy xye xy and Nx = exy xye xy, which implies that the differential equation is exact.
The final chapter deals with first-order differential equations. This book is a valuable resource for mathematicians, graduate students, and research workers. Table of Contents. Participants Preface I. Invited Papers A General Approach to Linear Problems for Nonlinear Ordinary Differential Equations Differential Relations Conditions for Boundedness of Systems of Ordinary Differential Equations
Differential equations arise in many problems in physics, engineering, and other sciences. The following examples show how to solve differential equations in a few simple cases when an exact solution exists. Separable first-order ordinary differential equations. Equations in the form = () are called separable and solved by () = and thus ∫ = ∫ (). Prior to dividing by (), one needs to check

Differential Equations Questions with Solutions Engg
Solutions of First-Order Volterra Type Linear

The final chapter deals with first-order differential equations. This book is a valuable resource for mathematicians, graduate students, and research workers. Table of Contents. Participants Preface I. Invited Papers A General Approach to Linear Problems for Nonlinear Ordinary Differential Equations Differential Relations Conditions for Boundedness of Systems of Ordinary Differential Equations
FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I: Introduction and Linear Systems David Levermore Department of Mathematics University of Maryland
6 I. Setting Up First-Order Differential Equations from Word Problems derivative at each point on a curve and where the curve begins, then you can reconstruct this solution curve.
Differential equations arise in many problems in physics, engineering, and other sciences. The following examples show how to solve differential equations in a few simple cases when an exact solution exists. Separable first-order ordinary differential equations. Equations in the form = () are called separable and solved by () = and thus ∫ = ∫ (). Prior to dividing by (), one needs to check
studied a variety of second order linear equations and they have saved us the trouble of finding solutions to the differential equations that often ap- pear in applications.
Linear Differential Equations of First Order. Page 1 Problems 1-2. Page 2 Problems 3-7. Definition of Linear Equation of First Order. A differental equation of type [y’ aleft( x right)y = fleft( x right),] where (aleft( x right)) and (fleft( x right)) are continuous functions of (x,) is called a linear nonhomogeneous differential equation of first order. We consider two
Ch 3.1: Second Order Linear Homogeneous Equations with Constant Coefficients A Consider the second order linear initial value problem where p, q are continuous on an open interval I containing t 0. In light of the initial conditions, note that y = 0 is a solution to this homogeneous initial value problem. Since the hypotheses of Theorem 3.2.1 are satisfied, it follows that y = 0 is the
A solution of a first order differential equation is a function f(t) that makes F(t,f(t),f ′ (t)) = 0 for every value of t. Here, F is a function of three variables which we label t, y, and ˙y.
The numerical solutions of linear integrodifferential equations of Volterra type have been considered. Power series is used as the basis polynomial to approximate the solution of the problem. Furthermore, standard and Chebyshev-Gauss-Lobatto collocation points were, respectively, chosen to collocate
Study differential equations questions with solutions online courses with multiple choice question (MCQs): wronskian is a, for bachelor degree and masters degree questions with choices difference, integration, determinant, differentiation with problem solving answer key to test study skills for online e-learning, formative assessment and jobs’ interview preparation tips. Learn second order
In this section we solve linear first order differential equations, i.e. differential equations in the form y’ p(t) y = g(t). We give an in depth overview of the process used to solve this type of differential equation as well as a derivation of the formula needed for the integrating factor used in the solution …
Differential Equations Problems With Solutions Pdf main ideas to solve certain differential equations, like first order scalar hence solutions to the
Solving First Order Linear Equations Today we will discuss how to solve a first order linear equation. Our technique will require close familiarity with the product and chain rules for derivatives, so we will
the equation into something soluble or on nding an integral form of the solution. First order PDEs a @u @x b @u @y = c: Linear equations: change coordinate using (x;y), de ned by the characteristic equation dy dx = b a; and ˘(x;y) independent (usually ˘= x) to transform the PDE into an ODE. Quasilinear equations: change coordinate using the solutions of dx ds = a; dy ds = b and du ds = c …

On the Cauchy Problem for First Order Discontinuous
First Order Differential Equations Practice Problem with

FIRST-ORDER ORDINARY DIFFERENTIAL EQUATIONS G ⇒ geometric interpretation of solutions ♦ Equations of higher order may be reduceable to first-order problems in special cases — e.g. when y or x variables are missing from 2nd order equations. …
Linear Differential Equations of First Order. Page 1 Problems 1-2. Page 2 Problems 3-7. Definition of Linear Equation of First Order. A differental equation of type [y’ aleft( x right)y = fleft( x right),] where (aleft( x right)) and (fleft( x right)) are continuous functions of (x,) is called a linear nonhomogeneous differential equation of first order. We consider two
the equation into something soluble or on nding an integral form of the solution. First order PDEs a @u @x b @u @y = c: Linear equations: change coordinate using (x;y), de ned by the characteristic equation dy dx = b a; and ˘(x;y) independent (usually ˘= x) to transform the PDE into an ODE. Quasilinear equations: change coordinate using the solutions of dx ds = a; dy ds = b and du ds = c …
First Order Differential Equations Practice Problem with Solutions FAQ PDF Download. Learn first order differential equations practice problem with solutions FAQ, engg math FAQ, competency based interview questions with MCQs based online test prep.
In this section we solve linear first order differential equations, i.e. differential equations in the form y’ p(t) y = g(t). We give an in depth overview of the process used to solve this type of differential equation as well as a derivation of the formula needed for the integrating factor used in the solution …
SECTION 15.1 Exact First-Order Equations 1093 Exact Differential Equations • Integrating Factors Exact Differential Equations In Section 5.6, you studied applications of differential equations to growth and decay problems. In Section 5.7, you learned more about the basic ideas of differential equa-tions and studied the solution technique known as separation of variables. In this chapter, you
Understand what the finite difference method is and how to use it to solve problems. What is the finite difference method? called boundary-value problems. In this chapter, we solve second-order ordinary differential equations of the form . f x y y a x b dx d y = ( , , ‘), ≤
Every rst order di erential equation to be considered here can be written can be written in the form P(x;y) usually guarantee that a di erential equation has a solution, in practice the solutions can seldom be written in closed form.” (I.e. there is no actual formula for the solution.) Thus the equations that are dealt with here are actually the exceptional ones. There are ve kinds of rst
Differential Equations Problems With Solutions Pdf main ideas to solve certain differential equations, like first order scalar hence solutions to the
6 I. Setting Up First-Order Differential Equations from Word Problems derivative at each point on a curve and where the curve begins, then you can reconstruct this solution curve.
Differential equations arise in many problems in physics, engineering, and other sciences. The following examples show how to solve differential equations in a few simple cases when an exact solution exists. Separable first-order ordinary differential equations. Equations in the form = () are called separable and solved by () = and thus ∫ = ∫ (). Prior to dividing by (), one needs to check
(1) First order equations: Variable-Separable Method. (2) Existence and uniqueness of solutions to initial value problems. (3) Continuation of solutions, Saturated solutions, and …

Solutions of First-Order Volterra Type Linear
First Order Differential Equations Practice Problem with

The final chapter deals with first-order differential equations. This book is a valuable resource for mathematicians, graduate students, and research workers. Table of Contents. Participants Preface I. Invited Papers A General Approach to Linear Problems for Nonlinear Ordinary Differential Equations Differential Relations Conditions for Boundedness of Systems of Ordinary Differential Equations
FIRST-ORDER ORDINARY DIFFERENTIAL EQUATIONS G ⇒ geometric interpretation of solutions ♦ Equations of higher order may be reduceable to first-order problems in special cases — e.g. when y or x variables are missing from 2nd order equations. …
SECTION 15.1 Exact First-Order Equations 1093 Exact Differential Equations • Integrating Factors Exact Differential Equations In Section 5.6, you studied applications of differential equations to growth and decay problems. In Section 5.7, you learned more about the basic ideas of differential equa-tions and studied the solution technique known as separation of variables. In this chapter, you
Solving First Order Linear Equations Today we will discuss how to solve a first order linear equation. Our technique will require close familiarity with the product and chain rules for derivatives, so we will
the equation into something soluble or on nding an integral form of the solution. First order PDEs a @u @x b @u @y = c: Linear equations: change coordinate using (x;y), de ned by the characteristic equation dy dx = b a; and ˘(x;y) independent (usually ˘= x) to transform the PDE into an ODE. Quasilinear equations: change coordinate using the solutions of dx ds = a; dy ds = b and du ds = c …
Every rst order di erential equation to be considered here can be written can be written in the form P(x;y) usually guarantee that a di erential equation has a solution, in practice the solutions can seldom be written in closed form.” (I.e. there is no actual formula for the solution.) Thus the equations that are dealt with here are actually the exceptional ones. There are ve kinds of rst
Differential equations arise in many problems in physics, engineering, and other sciences. The following examples show how to solve differential equations in a few simple cases when an exact solution exists. Separable first-order ordinary differential equations. Equations in the form = () are called separable and solved by () = and thus ∫ = ∫ (). Prior to dividing by (), one needs to check
A solution of a first order differential equation is a function f(t) that makes F(t,f(t),f ′ (t)) = 0 for every value of t. Here, F is a function of three variables which we label t, y, and ˙y.
Ch 3.1: Second Order Linear Homogeneous Equations with Constant Coefficients A Consider the second order linear initial value problem where p, q are continuous on an open interval I containing t 0. In light of the initial conditions, note that y = 0 is a solution to this homogeneous initial value problem. Since the hypotheses of Theorem 3.2.1 are satisfied, it follows that y = 0 is the
24 CHAPTER 2. METHODS FOR SOLVING FIRST ORDER ODES Solution: In this problem, M = ye xy and N = xe xy sin y. Thus, My = exy xye xy and Nx = exy xye xy, which implies that the differential equation is exact.
The numerical solutions of linear integrodifferential equations of Volterra type have been considered. Power series is used as the basis polynomial to approximate the solution of the problem. Furthermore, standard and Chebyshev-Gauss-Lobatto collocation points were, respectively, chosen to collocate
Understand what the finite difference method is and how to use it to solve problems. What is the finite difference method? called boundary-value problems. In this chapter, we solve second-order ordinary differential equations of the form . f x y y a x b dx d y = ( , , ‘), ≤
Study differential equations questions with solutions online courses with multiple choice question (MCQs): wronskian is a, for bachelor degree and masters degree questions with choices difference, integration, determinant, differentiation with problem solving answer key to test study skills for online e-learning, formative assessment and jobs’ interview preparation tips. Learn second order
Download the differential equations PDF here and learn about Differential equation solutions,Differential equations formulas and first order differential equations.Differential equations are mathematical equations that contain second derivatives.

On the Cauchy Problem for First Order Discontinuous
FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I

Every rst order di erential equation to be considered here can be written can be written in the form P(x;y) usually guarantee that a di erential equation has a solution, in practice the solutions can seldom be written in closed form.” (I.e. there is no actual formula for the solution.) Thus the equations that are dealt with here are actually the exceptional ones. There are ve kinds of rst
Understand what the finite difference method is and how to use it to solve problems. What is the finite difference method? called boundary-value problems. In this chapter, we solve second-order ordinary differential equations of the form . f x y y a x b dx d y = ( , , ‘), ≤
A solution of a first order differential equation is a function f(t) that makes F(t,f(t),f ′ (t)) = 0 for every value of t. Here, F is a function of three variables which we label t, y, and ˙y.
the equation into something soluble or on nding an integral form of the solution. First order PDEs a @u @x b @u @y = c: Linear equations: change coordinate using (x;y), de ned by the characteristic equation dy dx = b a; and ˘(x;y) independent (usually ˘= x) to transform the PDE into an ODE. Quasilinear equations: change coordinate using the solutions of dx ds = a; dy ds = b and du ds = c …
The numerical solutions of linear integrodifferential equations of Volterra type have been considered. Power series is used as the basis polynomial to approximate the solution of the problem. Furthermore, standard and Chebyshev-Gauss-Lobatto collocation points were, respectively, chosen to collocate
FIRST-ORDER ORDINARY DIFFERENTIAL EQUATIONS G ⇒ geometric interpretation of solutions ♦ Equations of higher order may be reduceable to first-order problems in special cases — e.g. when y or x variables are missing from 2nd order equations. …
In this section we solve linear first order differential equations, i.e. differential equations in the form y’ p(t) y = g(t). We give an in depth overview of the process used to solve this type of differential equation as well as a derivation of the formula needed for the integrating factor used in the solution …
6 I. Setting Up First-Order Differential Equations from Word Problems derivative at each point on a curve and where the curve begins, then you can reconstruct this solution curve.
The final chapter deals with first-order differential equations. This book is a valuable resource for mathematicians, graduate students, and research workers. Table of Contents. Participants Preface I. Invited Papers A General Approach to Linear Problems for Nonlinear Ordinary Differential Equations Differential Relations Conditions for Boundedness of Systems of Ordinary Differential Equations
Differential Equations Problems With Solutions Pdf main ideas to solve certain differential equations, like first order scalar hence solutions to the
Solving First Order Linear Equations Today we will discuss how to solve a first order linear equation. Our technique will require close familiarity with the product and chain rules for derivatives, so we will
SECTION 15.1 Exact First-Order Equations 1093 Exact Differential Equations • Integrating Factors Exact Differential Equations In Section 5.6, you studied applications of differential equations to growth and decay problems. In Section 5.7, you learned more about the basic ideas of differential equa-tions and studied the solution technique known as separation of variables. In this chapter, you
Linear Differential Equations of First Order. Page 1 Problems 1-2. Page 2 Problems 3-7. Definition of Linear Equation of First Order. A differental equation of type [y’ aleft( x right)y = fleft( x right),] where (aleft( x right)) and (fleft( x right)) are continuous functions of (x,) is called a linear nonhomogeneous differential equation of first order. We consider two

Differential Equations Questions with Solutions Engg
First Order Differential Equations Practice Problem with

(1) First order equations: Variable-Separable Method. (2) Existence and uniqueness of solutions to initial value problems. (3) Continuation of solutions, Saturated solutions, and …
The final chapter deals with first-order differential equations. This book is a valuable resource for mathematicians, graduate students, and research workers. Table of Contents. Participants Preface I. Invited Papers A General Approach to Linear Problems for Nonlinear Ordinary Differential Equations Differential Relations Conditions for Boundedness of Systems of Ordinary Differential Equations
24 CHAPTER 2. METHODS FOR SOLVING FIRST ORDER ODES Solution: In this problem, M = ye xy and N = xe xy sin y. Thus, My = exy xye xy and Nx = exy xye xy, which implies that the differential equation is exact.
First Order Differential Equations Practice Problem with Solutions FAQ PDF Download. Learn first order differential equations practice problem with solutions FAQ, engg math FAQ, competency based interview questions with MCQs based online test prep.
Differential Equations Problems With Solutions Pdf main ideas to solve certain differential equations, like first order scalar hence solutions to the
Solving First Order Linear Equations Today we will discuss how to solve a first order linear equation. Our technique will require close familiarity with the product and chain rules for derivatives, so we will
Every rst order di erential equation to be considered here can be written can be written in the form P(x;y) usually guarantee that a di erential equation has a solution, in practice the solutions can seldom be written in closed form.” (I.e. there is no actual formula for the solution.) Thus the equations that are dealt with here are actually the exceptional ones. There are ve kinds of rst
FIRST-ORDER ORDINARY DIFFERENTIAL EQUATIONS G ⇒ geometric interpretation of solutions ♦ Equations of higher order may be reduceable to first-order problems in special cases — e.g. when y or x variables are missing from 2nd order equations. …
Linear Differential Equations of First Order. Page 1 Problems 1-2. Page 2 Problems 3-7. Definition of Linear Equation of First Order. A differental equation of type [y’ aleft( x right)y = fleft( x right),] where (aleft( x right)) and (fleft( x right)) are continuous functions of (x,) is called a linear nonhomogeneous differential equation of first order. We consider two
Differential equations arise in many problems in physics, engineering, and other sciences. The following examples show how to solve differential equations in a few simple cases when an exact solution exists. Separable first-order ordinary differential equations. Equations in the form = () are called separable and solved by () = and thus ∫ = ∫ (). Prior to dividing by (), one needs to check
studied a variety of second order linear equations and they have saved us the trouble of finding solutions to the differential equations that often ap- pear in applications.

First Order Differential Equations Practice Problem with
On the Cauchy Problem for First Order Discontinuous

FIRST-ORDER ORDINARY DIFFERENTIAL EQUATIONS G ⇒ geometric interpretation of solutions ♦ Equations of higher order may be reduceable to first-order problems in special cases — e.g. when y or x variables are missing from 2nd order equations. …
the equation into something soluble or on nding an integral form of the solution. First order PDEs a @u @x b @u @y = c: Linear equations: change coordinate using (x;y), de ned by the characteristic equation dy dx = b a; and ˘(x;y) independent (usually ˘= x) to transform the PDE into an ODE. Quasilinear equations: change coordinate using the solutions of dx ds = a; dy ds = b and du ds = c …
First Order Differential Equations Practice Problem with Solutions FAQ PDF Download. Learn first order differential equations practice problem with solutions FAQ, engg math FAQ, competency based interview questions with MCQs based online test prep.
Every rst order di erential equation to be considered here can be written can be written in the form P(x;y) usually guarantee that a di erential equation has a solution, in practice the solutions can seldom be written in closed form.” (I.e. there is no actual formula for the solution.) Thus the equations that are dealt with here are actually the exceptional ones. There are ve kinds of rst
(1) First order equations: Variable-Separable Method. (2) Existence and uniqueness of solutions to initial value problems. (3) Continuation of solutions, Saturated solutions, and …

FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I
On the Cauchy Problem for First Order Discontinuous

24 CHAPTER 2. METHODS FOR SOLVING FIRST ORDER ODES Solution: In this problem, M = ye xy and N = xe xy sin y. Thus, My = exy xye xy and Nx = exy xye xy, which implies that the differential equation is exact.
Every rst order di erential equation to be considered here can be written can be written in the form P(x;y) usually guarantee that a di erential equation has a solution, in practice the solutions can seldom be written in closed form.” (I.e. there is no actual formula for the solution.) Thus the equations that are dealt with here are actually the exceptional ones. There are ve kinds of rst
A solution of a first order differential equation is a function f(t) that makes F(t,f(t),f ′ (t)) = 0 for every value of t. Here, F is a function of three variables which we label t, y, and ˙y.
Study differential equations questions with solutions online courses with multiple choice question (MCQs): wronskian is a, for bachelor degree and masters degree questions with choices difference, integration, determinant, differentiation with problem solving answer key to test study skills for online e-learning, formative assessment and jobs’ interview preparation tips. Learn second order
The final chapter deals with first-order differential equations. This book is a valuable resource for mathematicians, graduate students, and research workers. Table of Contents. Participants Preface I. Invited Papers A General Approach to Linear Problems for Nonlinear Ordinary Differential Equations Differential Relations Conditions for Boundedness of Systems of Ordinary Differential Equations
6 I. Setting Up First-Order Differential Equations from Word Problems derivative at each point on a curve and where the curve begins, then you can reconstruct this solution curve.
In this section we solve linear first order differential equations, i.e. differential equations in the form y’ p(t) y = g(t). We give an in depth overview of the process used to solve this type of differential equation as well as a derivation of the formula needed for the integrating factor used in the solution …
Understand what the finite difference method is and how to use it to solve problems. What is the finite difference method? called boundary-value problems. In this chapter, we solve second-order ordinary differential equations of the form . f x y y a x b dx d y = ( , , ‘), ≤
FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I: Introduction and Linear Systems David Levermore Department of Mathematics University of Maryland
Linear Differential Equations of First Order. Page 1 Problems 1-2. Page 2 Problems 3-7. Definition of Linear Equation of First Order. A differental equation of type [y’ aleft( x right)y = fleft( x right),] where (aleft( x right)) and (fleft( x right)) are continuous functions of (x,) is called a linear nonhomogeneous differential equation of first order. We consider two
Differential equations arise in many problems in physics, engineering, and other sciences. The following examples show how to solve differential equations in a few simple cases when an exact solution exists. Separable first-order ordinary differential equations. Equations in the form = () are called separable and solved by () = and thus ∫ = ∫ (). Prior to dividing by (), one needs to check
The numerical solutions of linear integrodifferential equations of Volterra type have been considered. Power series is used as the basis polynomial to approximate the solution of the problem. Furthermore, standard and Chebyshev-Gauss-Lobatto collocation points were, respectively, chosen to collocate