Solving equations involving variables on both sides requires careful manipulation, often utilizing worksheets for practice.

Numerous PDF resources offer examples, like 3x ⎼ 5 = 4a + 10, aiding comprehension of core principles.
These worksheets provide structured practice, reinforcing the steps of isolating variables and verifying solutions effectively.
Understanding the equality principle is crucial, alongside applying inverse operations to maintain balance in the equation.
Mastering these skills builds a strong foundation for tackling more complex algebraic problems with confidence and accuracy;
Consistent practice with worksheets is key to achieving fluency in solving equations efficiently and correctly.
What is an Equation?
An equation is a fundamental concept in algebra, representing a mathematical statement declaring the equality between two expressions.
These expressions are connected by an equals sign (=), signifying that the value on the left-hand side is identical to the value on the right-hand side.
Equations often contain variables, typically represented by letters like ‘x’ or ‘n’, which symbolize unknown values we aim to determine.
When dealing with solving equations, especially those with variables on both sides, understanding this core definition is paramount.
Worksheets focusing on these types of equations, often available as PDF downloads, frequently begin by reinforcing this basic principle.
For instance, an equation like ‘3x + 2 = x ⎼ 4’ asserts that the expression ‘3x + 2’ has the same value as ‘x — 4’.
The goal is to find the specific value of ‘x’ that makes this statement true, a process honed through practice with dedicated worksheets.
These worksheets help solidify the understanding that an equation isn’t just a problem, but a statement of balance.
Maintaining this balance through operations on both sides is key to successful equation solving.
Understanding Variables
Variables, commonly represented by letters like ‘x’, ‘y’, or ‘n’, are symbols that represent unknown quantities within an equation.
Their value isn’t fixed; instead, it’s the value we aim to discover through the process of solving the equation.
In equations with variables on both sides, such as ‘2k ⎼ 1 = k + 7’, ‘k’ is the variable we need to isolate and determine its value.
Worksheets dedicated to these equations, often in PDF format, emphasize the importance of treating variables consistently.
Any operation performed on one side of the equation must also be applied to the other side to maintain equality.
Understanding that a variable can take on different values is crucial; solving reveals the specific value that satisfies the equation.
These worksheets provide ample practice in manipulating equations to isolate the variable, reinforcing this fundamental concept.
Recognizing variables as placeholders for unknown numbers is the first step towards mastering algebraic equation solving.
Consistent practice with worksheets builds confidence in working with variables effectively.
The Goal of Solving Equations
The primary goal of solving equations is to isolate the variable – to determine the specific value that makes the equation true.
When dealing with variables on both sides, like ‘3x — 5 = 4a + 10’, this means manipulating the equation until the variable stands alone on one side.
Worksheets, frequently available as PDF downloads, provide structured practice in achieving this isolation through a series of steps.
These steps typically involve simplifying both sides, combining like terms, and applying inverse operations to ‘undo’ operations performed on the variable.
The ultimate aim is to arrive at a statement of the form ‘x = [a number]’, revealing the solution.
Solving equations isn’t just about finding an answer; it’s about understanding the relationship between the variable and other quantities.
Worksheets reinforce this understanding by presenting a variety of examples and practice problems.
Checking your solution by substituting it back into the original equation is a vital step to ensure accuracy.
Mastering this process empowers you to tackle more complex mathematical challenges effectively.

Basic Principles of Equation Solving
PDF worksheets emphasize the equality principle and inverse operations for solving equations.
Simplifying both sides and combining like terms are foundational skills for success.
Consistent practice builds confidence and accuracy.
The Equality Principle
The cornerstone of solving equations, including those with variables on both sides, is the equality principle.
This fundamental concept dictates that any operation performed on one side of an equation must be mirrored on the other side to maintain balance.
PDF worksheets consistently reinforce this principle through numerous practice problems, demonstrating how adding, subtracting, multiplying, or dividing both sides by the same value preserves the equation’s validity.
For instance, if you subtract 3 from the left side of an equation, you must also subtract 3 from the right side.
This ensures the two expressions remain equal.
Worksheets often present equations like 2x + 5 = x + 9, requiring students to apply this principle strategically.
Understanding this principle is vital for isolating the variable and arriving at the correct solution.
Without adhering to the equality principle, the equation becomes unbalanced, leading to an incorrect answer.
Therefore, worksheets emphasize careful and consistent application of this rule.
Mastering this concept is crucial for progressing to more complex algebraic manipulations.
Using Inverse Operations
Solving equations with variables on both sides heavily relies on employing inverse operations to isolate the variable.
Inverse operations “undo” each other – addition and subtraction, multiplication and division – maintaining the equality principle.
PDF worksheets are designed to build proficiency in recognizing and applying these operations effectively.
For example, if an equation includes ‘+7’ on one side, you’d use ‘-7’ as the inverse operation to eliminate it.
Worksheets often present problems like 3x + 2 = x + 8, prompting students to subtract ‘x’ from both sides, then subtract ‘2’ from both sides.
This systematic approach, reinforced through practice, simplifies the equation step-by-step.
The goal is to manipulate the equation until the variable stands alone on one side.
Worksheets provide ample opportunities to practice identifying the correct inverse operation for each term.
Consistent application of inverse operations, guided by PDF exercises, ensures accurate and efficient equation solving.
This skill is foundational for tackling more advanced algebraic concepts.
Combining Like Terms
Before applying inverse operations, solving equations often requires simplifying by combining like terms on each side.
Like terms share the same variable raised to the same power – for instance, ‘3x’ and ‘-5x’ are like terms.
PDF worksheets frequently include equations where this simplification is a crucial first step.
An example might be 2x + 5 ⎼ x + 3, where you combine ‘2x’ and ‘-x’ to get ‘x’, and ‘5’ and ‘3’ to get ‘8’.
Worksheets emphasize this skill, presenting problems like 4a + 7 — 2a + 1, requiring students to simplify to 2a + 8.
This process streamlines the equation, making it easier to isolate the variable using inverse operations.
Combining like terms ensures you’re working with the simplest form of the equation;
PDF practice materials provide numerous examples, reinforcing the concept and building confidence.
Mastering this step prevents errors and promotes a more efficient approach to equation solving.
Consistent practice with these worksheets solidifies understanding and improves algebraic manipulation skills.

Step-by-Step Guide to Solving
Worksheets guide students through simplifying, isolating variable terms, solving, and checking solutions.
Practice applying operations to both sides, combining like terms, and verifying answers accurately.
Consistent practice builds confidence in solving equations effectively.
Step 1: Simplify Both Sides
Simplifying both sides of the equation is the foundational first step in solving for the variable, and worksheets emphasize this crucial skill.
This involves combining like terms – those with the same variable and exponent – on each side of the equals sign independently.
For instance, in an equation like 3x + 5 — x = 2x + 10 — 3, you’d combine 3x and -x on the left to get 2x + 5, and 2x on the right, and 10 ⎼ 3 to get 2x + 7.
PDF worksheets often present equations with distribution, requiring you to apply the distributive property (e.g., 2(x + 3) = 2x + 6) before combining like terms.
Carefully applying these simplification techniques reduces the equation to its most basic form, making the subsequent steps of isolating the variable much easier to manage.
Remember to perform these operations on each side of the equation separately, maintaining the balance essential for a correct solution.
Many worksheets provide guided examples to illustrate this process, building confidence and accuracy.
Step 2: Isolate the Variable Term
Once both sides are simplified, the next step is to isolate the variable term – getting all terms containing the variable on one side of the equation.
This is achieved using inverse operations: addition and subtraction. If a variable term appears on both sides, choose one side to collect them on.
For example, if you have 2x + 5 = x + 7, subtract ‘x’ from both sides to get x + 5 = 7. Worksheets frequently present this scenario.
PDF practice materials emphasize applying the same operation to both sides to maintain equality – a fundamental principle.
The goal is to have a single term with the variable on one side and all constant terms on the other, setting the stage for solving for the variable.
Consistent practice with worksheets reinforces this concept, building proficiency in manipulating equations effectively.
Remember to carefully track your operations to avoid errors and ensure a correct solution.
Step 3: Solve for the Variable
With the variable term isolated, the final algebraic step is to solve for the variable itself. This typically involves using inverse operations – multiplication and division.
If the variable is being multiplied by a number, divide both sides of the equation by that number. Conversely, if it’s being divided, multiply both sides.
For instance, if you have 3x = 9, dividing both sides by 3 yields x = 3. Worksheets provide ample opportunities to practice this skill.
PDF resources often include problems requiring multiple steps, reinforcing the order of operations and careful manipulation of equations.
Always double-check your work to ensure accuracy. A common mistake is incorrectly applying the inverse operation or forgetting to apply it to both sides.
Consistent practice with worksheets builds confidence and fluency in solving for the variable efficiently and correctly.
Remember, the goal is to get the variable completely by itself on one side of the equation.
Step 4: Check Your Solution
After solving for the variable, a crucial step is to check your solution to ensure its accuracy. This involves substituting the obtained value back into the original equation.
If both sides of the equation are equal after the substitution, your solution is correct. If they are not equal, an error was made during the solving process.
Worksheets dedicated to solving equations often include space for this verification step, encouraging students to develop this habit.
PDF resources frequently present problems where checking the solution reveals errors in earlier steps, highlighting the importance of this process.
This step isn’t merely about confirming the answer; it’s about understanding the equation and the impact of the variable’s value.
Consistent practice with worksheets reinforces the importance of verification, building confidence and minimizing careless errors.
Always take the time to check – it’s a valuable safeguard against incorrect answers!

Types of Equations & Examples
Worksheets present equations with variables on both sides, including those needing distribution and fractions.
PDF resources offer diverse examples, like 3x — 5 = 4a + 10, for comprehensive practice.
These exercises build skills in isolating variables and mastering algebraic manipulation effectively.
Linear Equations with Variables on Both Sides
Worksheets focusing on linear equations with variables on both sides are fundamental for building algebraic proficiency. These PDF resources typically present problems requiring students to manipulate the equation to isolate the variable, employing inverse operations on both sides to maintain equality.
Examples commonly include problems like 2k ⎼ k = 7 ⎼ 8 or 3x, 5 = 4a + 10, demanding students combine like terms and strategically move variable and constant terms. The goal is to simplify the equation to a form where the variable is alone on one side.
Many worksheets also emphasize the importance of checking solutions by substituting the obtained value back into the original equation. This verification step reinforces understanding and minimizes errors. Practicing these equations builds a strong foundation for tackling more complex algebraic concepts, ensuring students grasp the core principles of solving for unknowns.
Resources like Maths4Everyone.com and Corbettmaths offer extensive practice and detailed solutions, aiding in self-assessment and targeted learning.
Equations with Distribution
Worksheets dedicated to equations requiring distribution present a more advanced challenge, often found in PDF format. These problems necessitate applying the distributive property before solving for the variable, adding an extra layer of complexity.
Examples frequently involve expressions like 2(x + 3) = 5x — 1, where students must first expand the left side to 2x + 6 before proceeding with standard equation-solving techniques. This involves multiplying the term outside the parentheses by each term inside.
These worksheets emphasize careful attention to detail, as errors in distribution can lead to incorrect solutions. Practicing these equations reinforces the order of operations and strengthens algebraic manipulation skills. Checking the solution remains crucial for verifying accuracy.
Resources often provide step-by-step guidance, demonstrating how to correctly distribute and then isolate the variable, building confidence and mastery. Consistent practice is key to becoming proficient in these types of equations.
Equations with Fractions
Worksheets focusing on equations containing fractions represent a significant step in algebraic problem-solving, commonly available as PDF downloads. These problems require students to manipulate fractional expressions to isolate the variable, demanding a strong understanding of fraction operations.
Examples might include equations like (x/2) + 1 = (3x/4) ⎼ 2. A common strategy involves multiplying both sides of the equation by the least common multiple (LCM) of the denominators to eliminate the fractions. In this case, the LCM of 2 and 4 is 4.
These worksheets often include problems with fractions on both sides of the equation, requiring careful application of the distributive property and combining like terms after clearing the fractions. Accuracy is paramount, as even small errors can lead to incorrect results.
Resources emphasize checking solutions by substituting them back into the original equation to ensure validity. Consistent practice with these worksheets builds proficiency and confidence in handling fractional equations.
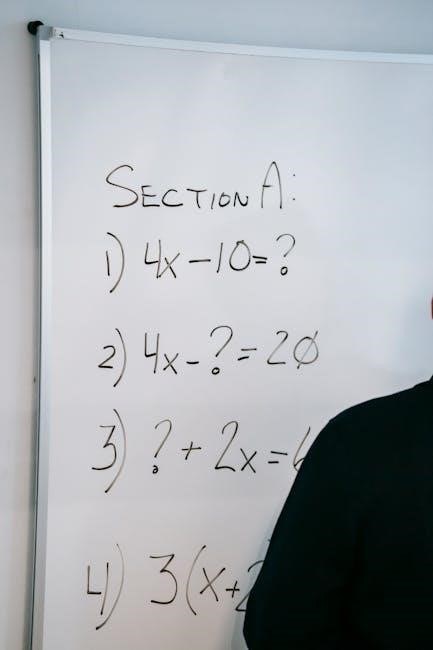
Worksheet Practice & Resources
PDF worksheets offer extensive practice for solving equations, with varied problems and solutions.
Resources like Maths4Everyone and Corbettmaths provide interactive quizzes and exam preparation materials.
These tools enhance understanding and skill development effectively.
Finding Free Printable Worksheets (PDF)
Numerous websites offer free, printable PDF worksheets specifically designed for practicing solving equations with variables appearing on both sides of the equals sign.
Maths4Everyone.com is a valuable resource, providing worksheets, videos, interactive quizzes, and even exam solutions, all focused on building algebraic proficiency.
Corbettmaths also presents a comprehensive collection of worksheets, categorized for easy navigation, and includes worked examples to guide students through the process.
Kuta Software is another excellent option, offering a wide range of algebra worksheets, including those targeting equations with variables on both sides, often with answer keys included for self-assessment.
Simply searching online for “solving equations with variables on both sides worksheets PDF” will yield a plethora of results, allowing you to choose resources that best suit your learning style and needs.
These worksheets typically include a variety of problem types, ranging from simple linear equations to more complex multi-step equations, providing ample opportunity for practice and skill development.
Remember to look for worksheets with answer keys to verify your solutions and identify areas where you may need further assistance.
Examples of Problems on Worksheets
Worksheets commonly feature problems like 3x — 5 = 4a + 10, requiring students to isolate ‘x’ by applying inverse operations to both sides of the equation;
Another frequent example is 2k — k = 7 — 8, focusing on combining like terms before proceeding with the isolation of the variable.

You’ll encounter equations such as 16 — 3n = 8 ⎼ 5n, demanding careful distribution and simplification before solving for ‘n’.
More complex examples include 4n — 1 = 3n + 2, testing the ability to maintain balance while moving variable and constant terms.
PDF worksheets often present a series of progressively challenging problems, starting with simpler linear equations and advancing to those requiring multiple steps.
Some worksheets include equations with no solution, prompting students to recognize inconsistencies and understand the concept of undefined solutions.
These problems reinforce the core principles of equation solving, building confidence and proficiency in algebraic manipulation.
Resources for Additional Practice
Maths4Everyone.com provides a wealth of resources, including worksheets, videos, and interactive quizzes specifically designed for solving equations with variables on both sides.
Corbettmaths offers comprehensive worksheets and detailed solutions, catering to various skill levels and learning styles, accessible via their website.
Numerous websites host free, printable PDF worksheets, allowing students to practice independently and reinforce their understanding of key concepts.
Khan Academy provides video tutorials and practice exercises, offering a structured approach to mastering equation-solving techniques.
IXL Learning offers skill-building exercises with immediate feedback, helping students identify and address areas where they need improvement.
Teachers Pay Teachers features a variety of worksheets created by educators, providing diverse practice opportunities.
Utilizing these resources alongside PDF worksheets ensures a well-rounded and effective learning experience.

Common Mistakes to Avoid
Avoid forgetting to apply operations to both sides, and carefully combine like terms when using worksheets.
Incorrect application leads to inaccurate solutions; double-check each step for precision.
Consistent practice minimizes errors!
Forgetting to Apply Operations to Both Sides
A prevalent error when solving equations, particularly when utilizing worksheets focused on variables on both sides, is neglecting to perform the same operation on both sides of the equation.
The equality principle dictates that maintaining balance is paramount; any action taken on one side must be mirrored on the other.
For instance, if adding 5 to the left side of an equation, you must also add 5 to the right side to preserve the equality.
PDF worksheets often present equations like 2x + 3 = x + 7, where students might correctly subtract ‘x’ from the left, but fail to do so on the right, disrupting the balance.
This oversight leads to an incorrect solution.
Carefully reviewing each step and consciously applying operations to both sides is crucial.
Many worksheets include ‘check your answer’ sections precisely to identify this type of error, encouraging students to substitute their solution back into the original equation.
Consistent practice and mindful application of the equality principle are key to avoiding this common pitfall.
Incorrectly Combining Like Terms
A frequent mistake encountered while solving equations with variables on both sides, especially when working through worksheets, involves incorrectly combining like terms.
Students may erroneously add or subtract terms that aren’t comparable, leading to a flawed simplification of the equation.
For example, in an equation like 3x + 2y – x + 5y = 10, combining ‘3x’ and ‘2y’ would be incorrect; only ‘3x’ and ‘-x’ or ‘2y’ and ‘5y’ can be combined.
PDF worksheets often feature equations designed to test this skill, such as 4a + 5b – 2a + b = 12, where accurate simplification is vital.
This error often stems from a misunderstanding of variable representation and the concept of ‘like’ terms.
Careful attention to the variable and its coefficient is essential.
Reviewing the basics of algebraic expressions and practicing simplification exercises on worksheets can significantly reduce this error.
Always remember to combine terms with the same variable only.

Advanced Concepts
PDF worksheets extend to multi-step equations and scenarios with no solution, challenging students beyond basic variable manipulation.
These advanced problems build upon foundational skills, demanding a deeper understanding of algebraic principles.
Multi-Step Equations
Multi-step equations, frequently found on solving equations with variables on both sides worksheets PDF, demand a systematic approach beyond simple isolation techniques.
These problems often involve combining like terms on one or both sides before applying the equality principle and inverse operations.
Worksheets progressively introduce distribution, requiring students to expand expressions like 2(x + 3) before proceeding with standard solving methods.
Fractions also appear, necessitating finding common denominators to eliminate them and simplify the equation.
Examples on these PDFs include problems like 5x + 2(x ⎼ 1) = 17, guiding students through each step of simplification and solution.
Mastering these skills requires diligent practice, reinforcing the order of operations and the importance of applying transformations to both sides.
Successfully navigating multi-step equations builds a robust foundation for tackling more complex algebraic challenges encountered in higher-level mathematics.
Consistent use of worksheets ensures a thorough understanding of these crucial concepts.
Equations with No Solution
Certain equations with variables on both sides, often presented on solving equations with variables on both sides worksheets PDF, surprisingly yield no solution.
These occur when, after applying all valid algebraic manipulations – combining like terms, using inverse operations – a contradiction arises.
For instance, simplifying an equation might lead to a statement like 2 = 5, which is demonstrably false, indicating no value of the variable can satisfy the original equation.
Worksheets intentionally include these scenarios to challenge students to recognize such inconsistencies and correctly identify the lack of a solution.
Examples might involve equations like 3(x + 2) = 3x + 1, where simplification reveals the contradiction.
Understanding this concept is crucial; it’s not a matter of incorrect solving, but recognizing inherent impossibility.
These PDF resources emphasize careful simplification and logical deduction to identify these ‘no solution’ cases effectively.
Mastering this skill demonstrates a deeper understanding of algebraic principles beyond simply finding numerical answers.